【Mathematica下载】Mathematica激活版 v5.0 官方版
软件介绍
Mathematica破解版是一款非常强大的数学计算软件,与MATLAB、Maple合称世界三大计算软件,这款软件可以很好的将数值和符号计算引擎、编程语言、文本系统等许多内容相结合,从而满足各个领域对科学计算的需求。
软件特色
超过 500 种的新函数,大幅拓宽了全新和既存领域的覆盖范围
用算法生成、导入三维模型,并使用本地或云端三维打印机直接打印模型
为音乐和语音处理分享了全新的计算音频合成、处理和分析功能
全新的神经网络框架使用户可以利用 GPU 加速的深度学习平台
拓展和增强的机器学习功能,包括特征抽取和贝叶斯最优化
对Wolfram Cloud、网页操作和数据存储进行了众多扩展和改进
大量新型可视化系列涵盖从统计,几何到解剖学等众多领域,进一步完善了演示的选项
强化了既存的处于行业领先地位的符号、数值和几何方面的性能及特性
扩展的地理学,包括新型地理数据实体、地图背景和投影以及更多内容
全新的计算摄影学,附加更多用于图像和信号处理的工具
用于随机矩阵、时间序列以及概率和统计中量值的全新和增强支持
用于云端、桌面和嵌入系统间异步通信的实验性 Wolfram信道框架
软件功能
基本运算
常用数学函数
数值设定
四个处理指令
多项式转换
多母分子运算
转换函数
函数指数运算
次方成绩
软件界面
前端由 Theodore Gray 设计,分享了一个 GUI,它使得用户可以创建并且编辑一个“笔记本文档”,该笔记本文档可以包含程序代码和其它格式化的文本(比如公式、图像、GUI组件、表格、声音等),并且支持标准文字处理功能。所有的内容和格式都可以通过算法生成或者通过交互式方法进行编辑。
文档可以使用层次式单元进行结构化处理,这样便于对文档划分章节。文档也可以表示为幻灯片形式,便于进行演讲。笔记本与其内容均以 Mathematica 表达式的形式存储,并且可用使用 Mathematica 程序进行创建、编辑和修改,而且还可以转化为其它格式,比如 TeX 或者 XML。
mathematica安装方法
1、等待mathematica下载完成,将软件包解压后运行安装程序。如下直接单击【next】
2、如需设置mathematica安装路径,单击【browse】进行设置。
3、直接跳过,单击【next】
4、直接单击【next】
5、确认mathematica安装信息无误后选择【install】,然后等其安装完毕即可。
mathematica使用方法
1).请先安装好 Mathematica 5.0 原版程序,并退出原版程序的运行。
2).将补丁安装到 Mathematica 5.0 原版程序所在的目录下。
1、特殊字符的输入
Mathematica还分享了用以输入各种特殊符号的工具样。基本输入工具样包含了常用的特殊字符(上图),只要单击这些字符按钮即可输入。若要输入其它的特殊字符或运算符号,必须使用从FILE菜单中选取 Complete Characters工具栏,如下图
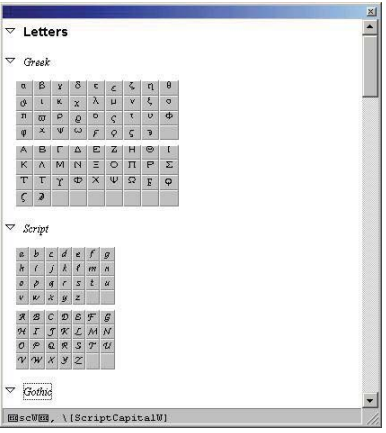
单击符号后即可输入。
2、数学常数
Mathematica中定义了一些常见的数学常数,这些数学常数都是精确数,例如表示圆周率。

数学常数可用在公式推导和数值计算中。在数值计算中表示精确值,如:

Mathematica常用数学函数
Sin[x],Cos[x],Tan[x],Cot[x],Sec[x],Csc[x] 三角函数,其引数的单位为弧度
Sinh[x],Cosh[x],Tanh[x],… 双曲函数
ArcSin[x],ArcCos[x],ArcTan[x] 反三角函数
ArcCot[x],ArcSec[x],ArcCsc[x]
ArcSinh[x],ArcCosh[x],ArcTanh[x],… 反双曲函数
Sqrt[x] 根号
Exp[x] 指数
Log[x] 自然对数
Log[a,x] 以a为底的对数
Abs[x] 绝对值
Round[x] 最接近x的整数
Mathematica学习笔记
1.0 Mma严格区分大小写,一般内建函数首字母必须大写,有时一个函数名由几个单词构成,则每一个单词的首字母也必须大写,如求局部极小值F inMinimum[f[x],{x,x0}]等。2.0 在mma中,函数名和变量名之间分隔符用[],不是一般数学上的();
3.0 在交互界面,使用?可以查询运算符,函数和命令定义。在mma中,基本的数据类型有4种,整数,有理数,实数和复数。
如果计算机内存足够大,mma可以表示任意长度的精确实数,可以简化分数,可以科学计数法,可以复数。Mma可以进行数据转换,%表示上一个输出结果。N[x,n]将x转换成近似实数,精度n,默认6位,Rationalize[x],给出近似实数。Mma定义了一些常见的数学常数。
数的输出形式
在数的输出中可以使用转换函数进行不同数据类型和精度的转换。另外对一些特殊要求的格式还可以使用如下的格式函数:
NumberForm[expr,n] 以n位精度的实数形式输出实数expr
ScientificForm[expr] 以科学记数法输出实数expr
EngineergForm[expr] 以工程记数法输出实数expr
变量
在mma中,函数和命令都是以大写字母开始的标识符,为了不和它们混淆,我们自定义的变量应该以小写字母开始,后跟数字和字母的组合,长度不限。
在mma中,用等号给变量赋值(或:=)变量,同一个变量可以表示数组,数字,表达式,甚至一个图形,=是立即赋值, :=是延迟赋值。要清楚在用等号。清除上一次的变量值,使用Clear[var]函数。可以使用变量替换来计算表达式的值,即 expr/.x->xval。
函数定义
立即定义函数的语法如下,F[x_]=expr 函数名F,变量x,expr是表达式,在执行时候会把expr中的x替换成f的自变量x,自变量具有局部性,只对所在函数起作用。
Mma可以计算极限,导数,偏导数,积分等。Mma可以级数展开,可以求解一元二次方程,二元一次方程,微分方程等号各种方程。其实mma求强大的功能在于画图。
下面有些代码是网上copy的,我玩的也不是很牛。
输入 Plot[{Sin[x],Cos[x],Tan[x]},{x,-Pi,Pi}]
输入 ParametricPlot[{Sin[t],Sin[2 t]},{t,0,2 Pi}]
输入 Plot3D[{Sqrt[(1-x^2 -y^2)]},{x,-1,1},{y,-1,1}
]输入 ParametricPlot3D[{u Cosu,u Sinu,u Sin[v+u]},{u,0,4 Pi},{v,0,2 Pi},PlotPoints->{60,12}]
输入 RegionPlot[(x^2 + y^2 – 1)^3 – x^2 *y^3 <= 0, {x, -1.5, 1.5}, {y, -3/2,
3/2}, PlotStyle -> Red]
输入 ContourPlot3D[(2x^2 + y^2 + z^2 – 1)^3 – (x^2 + y^2)/10 – y^2z^3 ==
0, {x, -1.5, 1.5}, {y, -1.5, 1.5}, {z, -1.5, 1.5}, PlotPoints -> 30,
Axes -> True, Lighting -> Automatic,
ContourStyle -> {RGBColor[1, 0, 0]}, Mesh -> None]
输入 Rose[x_,theta_]:=Module[{phi=(Pi/2) Exp[-theta/(8 Pi)],X=1-(1/2) ((5/4) (1-Mod[3.6 theta,2 Pi]/Pi)2-1/4)2,y,r},y=1.95653 x^2 (1.27689 x-1)^2 Sin[phi];
r=X (x Sin[phi]+y Cos[phi]);
{r Sin[theta],r Cos[theta],X (x Cos[phi]-y Sin[phi])}]
Manipulate[Show[ParametricPlot3D[Evaluate@Rose[x,theta],{x,0,1},{theta,-2 Pi,th},Mesh->None,PerformanceGoal->”Speed”,PlotPoints->100,PlotStyle->{clr},ImageSize->{450,400},PlotRange->{{-1,1},{-1,1},{-1.6,1}},Boxed->False,Axes->Fase],Graphics3D[{Green,Cylinder[{{0,0,-.05},{0,0,-10}},.1]}]],{{th,15 Pi,”花瓣的变化”},Pi,15 Pi},{{clr,Red,”花瓣的颜色”},Red},SaveDefinitions->True]
输入 ContourPlot3D[(x^2 + 9/4 y^2 + z^2 – 1)^3 – x2*z3 – 9/80 y2*z3 ==
0, {x, -1.5, 1.5}, {y, -1.5, 1.5}, {z, -1.5, 1.5}, Mesh -> None,
BoxRatios -> 1, ContourStyle -> {Red}, PlotPoints -> 200,
Axes -> None, Boxed -> False
Mathematica常见问题
首先, 最容易犯的就是关键字冲突. 当然系统内建的函数名我们就不能再使用, 这里如(C, Pi, I, Pi)已经被系统占用了. 初学的时候也会常见到想要赋值给C. 那么系统就就报错, 说符号C式被保护起来的.
C= 2
Set::wrsym: 符号 C 被保护. >>
2
D= 8
Set::wrsym: 符号 D 被保护. >>
8
再来, 大小写字母被确认为不同的字符, 并且内置的符号首字母都是大写且遵循了驼峰风格. 那这里的一个经验就是我们可以利用首字母小写来定义变量或者函数, 用以区别.
在使用的时候大小写字母被确认为不同的字符, 通常会犯的一种错误就是如下图所示那样. 虽然首字母是大写, 但是中间应该大写输入成了小写.
Arcsin[1]
Arcsin[1]
ArcSin[1]
\[Pi]/2
Texture
还有, 一种错误是初学者常犯的, 就是没有意识到空格就是乘法 . Mathematica 下乘法可以用一个空格来表示. 下面几种方法都是等价的
a*b
a b
a b
a b
a*b
a b
Times[a,b]
a b
还有一个常犯的错误, 就是编写代码的时候, 括号不匹配. 这个跟 Mathematica 独特的表示相关: [] 扩住要计算的参数 . 当然对于复杂点的代码, 所要用到的大括号就会非常复杂, 在修改或者输入的时候常常出现括号不匹配的情况. 在 Mathematica 9 这样的情况会稍微好一点, 会有一点语法颜色的提示. 但一个最好的习惯就是使用模板输入, 这样的就不容 易少输入一个大括号.
请熟悉这个大括号环境, 尽管刚开始可能稍微有点难以适应.
再来关注最后一个常犯的错误, 用完所设置的变量后,就立即清除该变量的值.需要注意的是在,对于所有的变量赋值,如果我们没有清除或改写它们的话,在 Mathematica 的同一个进程中所赋值保持不变. 常犯的错误是在后面使用 x 时忘记或误用了前面 x 的赋值. 查看下面代码所绘制的图形中的标题, 并不是我们所期望的.

Precision[x] == Accuracy[x] + RealExponent[x] holds for any arbitrary precision number.E.g.try x = 4.7`20. 转自Twitter # Mathematica Tip #
Maple、MATLAB、MathCAD和Mathematica优缺点比较
Maple V 系统
Maple V是由Waterloo大学开发的数学系统软件,它不但具有精确的数值处理功能,而且具有无以伦比的符号计算功能。Maple V的符号计算能力还是MathCAD和MATLAB等软件的符号处理的核心。Maple分享了2000余种数学函数,涉及范围包括:普通数学、高等数学、线性代数、数论、离散数学、图形学。它还分享了一套内置的编程语言,用户可以开发自己的应用程序,而且Maple自身的2000多种函数,基本上是用此语言开发的。
Maple采用字符行输入方式,输入时需要按照规定的格式输入,虽然与一般常见的数学格式不同,但灵活方便,也很容易理解。输出则可以选择字符方式和图形方式,产生的图形结果可以很方便地剪贴到Windows应用程序内。
5个星的数学软件,纯粹数学的巨人,如果想做数学和应用数学的能力(数值的除外)其是最好的选择。但是此软件二次开发能力不好,仅把软件的发展目标放在数学上,不想向其它领域发展。Maple自带的语言较容易理解,就像用英语说话一样。
优势:
符号计算非常强大,和Mathematica相比各有千秋
许多多项式操作比Mathematica更快
一些符号积分Maple也有速度优势(特别是不定积分),不过有时返回的结果没有Mathematica给出的更严谨、鲁棒性好,能算的积分类型没有Mathematica多
Maple的“适应性”更好,有的问题Mathematica需要一定的预处理才能算的更快,得出满意的结果
Maple更擅长(偏)微分方程,(其实Maple和Mathematica都能解一些对方解不了的一些特殊微分方程)
可以带步骤求解一些问题,Mathematica需要第三方的Package或借助WolframAlpha
上手较快,一些常见的操作无需命令,通过右键菜单就能完成
缺点:
界面有点卡(基于Java swing),经典界面流畅但是很土
自带的代数方面的package比较丰富
化简能力,不等式求解,逻辑系统较Mathematica逊色一些
数值计算总体上比Matlab和Mathematica差一些
高精度和大数计算方面强于Matlab弱于Mathematica
统计方面有些薄弱
MATLAB 系统
MATLAB原是矩阵实验室(Matrix Laboratory),在70年代用来分享Linpack和Eispack软件包的接口程序,采用C语言编写。从80年代出现3.0的DOS版本,逐渐成为科技计算、视图交互系统和程序语言。MATLAB可以运行在十几个操作平台上,比较常见的有基于Windows 9X/NT、OS/2、Macintosh、Sun、Unix、Linux等平台的系统。
MATLAB程序主要由主程序和各种工具包组成,其中主程序包含数百个内部核心函数,工具包则包括复杂系统仿真、信号处理工具包、系统识别工具包、优化工具包、神经网络工具包、控制系统工具包、μ分析和综合工具包、样条工具包、符号数学工具包、图像处理工具包、统计工具包等。而且5.x版本还包含一套几十个的PDF文件,从MATLAB的使用入门到其他专题应用均有详细的介绍。
MATLAB是数值计算的先锋,它以矩阵作为基本数据单位,在应用线性代数、数理统计、自动控制、数字信号处理、动态系统仿真方面已经成为首选工具,同时也是科研工作人员和大学生、研究生进行科学研究的得力工具。MATLAB在输入方面也很方便,可以使用内部的Editor或者其他任何字符处理器,同时它还可以与Word6.0/7.0结合在一起,在Word的页面里直接调用MATLAB的大部分功能,使Word具有特殊的计算能力。
优势:
线性代数和数值计算方面优势显著,
向量化运算往往比同类软件更快,
拥有超多工具箱,仿真,图像处理,信号处理,金融,统计,优化……
程序语言比较易学,编辑和调试环境不错
方便构建GUI
缺点:
不是原生支持符号计算(符号计算远不止是推导公式),新版的mupad内核还不错,但是和Mathematica、Maple比有明显差距,不论是深度、广度和速度
递归特别慢,比Mathematica和Maple以及常见的脚本语言都慢
在一些数学领域相对薄弱,如数论,图论,离散数学等
高精度和大数计算比较慢(如精确计算100万的阶乘或π的前500万位)
工具箱之间的协作能力不是很好
界面不太好看(新版R2013a的Ribbon界面不错)
缺省画图不美观,锯齿,系统函数命名不够规范
MathCAD 系统
MathCAD是美国Mathsoft公司推出的一个交互式的数学系统软件。从早期的DOS下的1.0和Windows下的4.0版本,到今日的8.0版本,功能也从简单的数值计算,直至引用Maple强大的符号计算能力,使得它发生了一个质的飞跃。
MathCAD是集文本编辑、数学计算、程序编辑和仿真于一体的软件。MathCAD7.0 Professional(专业版)运行在Win9X/NT下,它的主要特点是输入格式与人们习惯的数学书写格式很近似,采用WYSWYG(所见所得)界面,特别适合一般无须进行复杂编程或要求比较特殊的计算。MathCAD 7.0 Professional 还带有一个程序编辑器,对于一般比较短小,或者要求计算速度比较低时,采用它也是可以的。这个程序编辑器的优点是语法特别简单。
MathCAD可以看作是一个功能强大的计算器,没有很复杂的规则;同时它也可以和Word、Lotus、WPS2000等字处理软件很好地配合使用,可以把它当作一个出色的全屏幕数学公式编辑器。
MathCAD是美国Mathsoft公司推出的一个交互式的数学系统软件。从早期的DOS下的1.0和Windows下的4.0版本,到今日的8.0版本,功能也从简单的数值计算,直至引用Maple强大的符号计算能力,使得它发生了一个质的飞跃。
Mathematica 系统
Mathematica是由美国物理学家Stephen Wolfram领导的Wolfram Research开发的数学系统软件。它拥有强大的数值计算和符号计算能力,在这一方面与Maple类似,但它的符号计算不是基于Maple上的,而是自己开发的。
Mathematica的基本系统主要是用C语言开发的,因而可以比较容易地移植到各种平台上,Mathematica是一个交互式的计算系统,计算是在用户和Mathematica互相交换、传递信息数据的过程中完成的。Mathematica系统所接受的命令都被称作表达式,系统在接受了一个表达式之后就对它进行处理,然后再把计算结果返回。Mathematica对于输入形式有比较严格的规定,用户必须按照系统规定的数学格式输入,系统才能正确地处理,不过由于3.0版本引入输入面板,并且可以修改、重组输入面板,因此以前版本输入指令时需要不断切换大小写字符的繁琐方式得到很好的改善。3.0版本可以用各种格式保存文件和剪贴内容,包括RTF、HTML、BMP等格式。
Mathematica的符号功能是最强的,其运行构架也是最优的。它的构架由核心系统与前端系统构成。两个系统既合作又独立,这比Matlab的构架要合理。Mathematica是专为研究人员开发的。横向比较的话,Mathematica的符号能力比Maple强很多,Maple基本上是为中学生与大学生之学习研发的,不适合进行物理学与技术科学的运演;而Mathematica是最好的物理学科研的工具,Matlab是最好的技术科学数值求解的工具。
4个星的“数学”软件,在数学二字上加引号是因为他已经超越了纯粹数学的范畴,这主要表现在他不断开发的面向于不同学科的工具包。就做数学和应用数学的能力来说Mathematica不如Maple(并不是说其做不了,不怕麻烦编程序也能做,但是话说回来基本的东西都编程序的话,那么和Fortran之类的语言没什么区别了)。另一个问题是Mathematica的内核不如Maple稳定(计算速度较Maple慢,我是说纯粹的计算时间,不是输入命令的时间,目前的Maple的Java界面比较失败,让人感觉算Maple算得慢,其实不是这样的)。Mathematica的诱人之处是与其它数值软件相比可以做符号运算,与Maple相比二次开发性好,工具包比Maple做的好。此外,其自带的语言是面向对象的,很厉害,很灵活。
优势:
符号计算非常强大,可解的方程类型最广泛
非常强大和灵活的语言,完成相同的工作,和同类语言相比代码量往往最少
语言高度统一,支持相当多的编程范式,过程式、函数式、元编程,逻辑编程、基于规则…
循环比较慢,可以用Compile加速,或使用Map、Table、Nest等代替循环
许多内置函数具备AAS机制(AutomaticAlgorithmSelection)
擅长高精度和大数计算,图形方面的函数很丰富,默认画图比Matlab和Maple更好看
界面美观,输入公式很方便
帮助文档很友好
缺点:
价格较高,比matlab更贵(Matlab的价格取决于你要哪些工具箱)
向量化的操作比Matlab稍慢,有时比Matlab更耗内存
代码调试不是很方便,但可以用Wolfram Workbench(基于Eclipse的IDE)改善
程序语言学习曲线陡峭,排除熟悉Scheme、Haskell等函数式语言或者作为高级计算器使用的人
(Mathematica的语法和常见的过程式程序语言有较大不同,虽然也可以作为过程式语言来用,但代码的和速度和优雅程度就大打折扣了)
四种软件的比较
选用何种数学软件?如果仅仅是要求一般的计算或者是普通用户日常使用,首选的是MathCAD,它在高等数学方面所具有的能力,足够一般客户的要求,而且它的输入界面也特别友好。
如果要求计算精度、符号计算和编程方面的话,最好同时使用Maple和Mathematica,它们在符号处理方面各具特色,有些Maple不能处理的,Mathematica却能处理,诸如某些积分、求极限等方面,这些都是比较特殊的。如果要求进行矩阵方面或图形方面的处理,则选择MATLAB,它的矩阵计算和图形处理方面则是它的强项,同时利用MATLAB的NoteBook功能,结合Word6.0/7.0的编辑功能,可以很方便地处理科技文章。
如果仅仅是要求一般的计算或者是普通用户日常使用,首选的是MathCAD,它在高等数学方面所具有的能力,足够一般客户的要求,而且它的输入界面也特别友好。如果要求计算精度、符号计算和编程方面的话,最好同时使用Maple和Mathematica,它们在符号处理方面各具特色,有些Maple不能处理的,Mathematica却能处理,诸如某些积分、求极限等方面,这些都是比较特殊的。如果要求进行矩阵方面或图形方面的处理,则选择MATLAB,它的矩阵计算和图形处理方面则是它的强项,同时利用MATLAB的NoteBook功能,结合Word的编辑功能,可以很方便地编辑科技文章。
选用何种数学软件?
如果仅仅是要求一般的计算或者是普通用户日常使用,首选的是MathCAD,它在高等数学方面所具有的能力,足够一般客户的要求,而且它的输入界面也特别友好。
如果要求计算精度、符号计算和编程方面的话,最好同时使用Maple和Mathematica,它们在符号处理方面各具特色,有些Maple不能处理的,Mathematica却能处理,诸如某些积分、求极限等方面,这些都是比较特殊的。
如果要求进行矩阵方面或图形方面的处理,则选择MATLAB,它的矩阵计算和图形处理方面则是它的强项,同时利用MATLAB的NoteBook功能,结合Word6.0/7.0的编辑功能,可以很方便地处理科技文章。
mathematica 值得信赖,国外很多著名的大学都在用它作解析计算和公式的推导,证明,算法的研究,非常好的数学研究软件,我个人认为是No.1。它的数学分析可视化无与伦比。综合性能和另一个著名的软件Maple相比,有过之而无不及,要知道世界上绝大部分的量子物理,天体物理论文中的公式推导都由它完成,绝对高端但又易用,是数学,力学,物理研究人员的好帮手,甚至它的数值计算也完全可以应付学术研究。mathematica 和Maple 的最新版本在用户公式的输入上都有很大改进,更加方便,随意。
北美不少Top大学的弹性力学,板壳理论,有限元等数学力学理论课的作业和Project都要求用它来完成。我个人认为,作为计算力学的工作者,从掌握语言的角度来讲,只要掌握3种计算语言足够了,mathematica用来作解析法和数学模型的研究,Matlab用来实现数值算法(当然仍然可以还用mathematica), Fortran用来写可执行源代码。没必要把自己陷入众多的语言和计算软件之中,没有意义的。
符号计算:积分是Mathematica强,化简也是Mathematica的强项。有些Mathematica可以直接积分的,Maple却要用置换积分。微分方程的解析解是Maple强些,有很多微分方程的解析解Maple能算出,Mathematica却不能。根据文献,Maple可以解Kamke书上的97%的微分方程。
另外,积分方程也是Maple强些,因为Maple里内带intsolve函数,因此可以算出解析解。例如eq:=f(x)=2*x^2- x+Int(f(t),t=0..2)的关于f(x)的积分方程,Maple得出intsolve(eq,f(x)) => 2*x^2-x-10/3,而Mathematica解不了。
数值计算:数值计算是Mathematica好,主要差别在于有时间差的微分方程的数值解只有Mathematica可以解,再者从Mathematica 9开始可以解概率微分方程了,Maple还不行。总体来说Mathematica在这个方面比Maple强。
语言方面:由于Maple像C语言,Maple比Mathematica简单,Matlab移植也是Maple比Mathematica强多了。
线性代数:线性代数是Mathematica强,有些Maple不能做的Mathematica能做,再者Mathematics比Maple快。
计算代数几何:计算代数是Maple的超强项,强暴于Mathematica,特别是PolynomialIdeals操作等,微分多元环操作Mathematica是没有的,再者多项式计算也是Maple快于Mathematica。所以,代数计算是Maple大大超过mathematica。
GUI:总体内容Maple的GUI像LATEX一样漂亮,而Mathematica适应于编程GUI。
Maple和Mathematica都得用,微分,积分方程基本可以拜托Maple了(概率微分方程拜托Mathematical)。
积分拜托给Mathematica。
计算代数几何,GUI,Programming拜托给Maple。
线性代数,数值计算拜托给Matlab和Mathematica。
更新日志
优化部分功能
下载仅供下载体验和测试学习,不得商用和正当使用。

发表评论